加工の必須知識【機械製図の幾何公差】記号の意味や書き方を説明

今回は機械製図の幾何公差について説明します。

幾何公差は「機械」を作る上で、設計する人、部品を加工をする人、それぞれに必要な知識です。初心者の頃はあまり気にしないと思いますが、知識が深まるにつれ必要性を感じると思います。

最後まで読むと幾何公差の書き方、図面の幾何公差の意味が理解できるようになります。

幾何公差とは

まず、公差とは許容される誤差のことです。
公差は3つに分類されます。

• 寸法公差
  • 寸法を管理
    
• はめあい公差
  • 軸と穴の寸法を管理
    
• 幾何公差
  • 形状を管理

幾何公差は他の公差に比べ、使われる頻度は少ない公差です。理由は、寸法公差とはめあい公差である程度の形状は表現できるためです。その2つの公差で表現しきれない場合、幾何公差を使うため、必然的に厳しい精度を要求されることが多くなります。

幾何公差には単独形体、関連形体があります。

• 単独形体はその形体単独で指定できるもの
  
• 関連形体は相手（データム）との関連を指定するもの

幾何公差の一覧

６０形体	公差の種類	公差の名称	記号	定義（JIS）
単独 形体	形状 公差	真直度		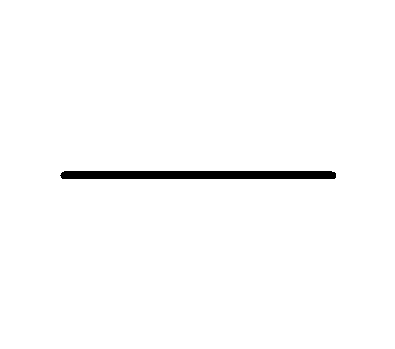直線形体の幾何学的に正しい直線からの狂いの大きさ
〃	〃	平面度		平面形体の幾何学的に正しい平面からの狂いの大きさ
〃	〃	真円度		円形形体の幾何学的に正しい円からの狂いの大きさ
〃	〃	円筒度		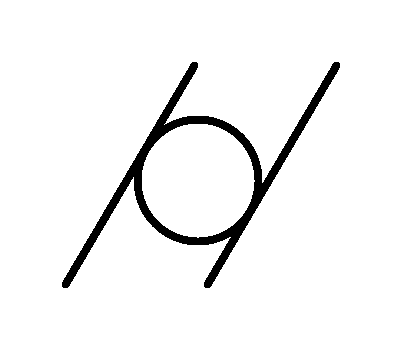円筒形体の幾何学的に正しい円筒からの狂いの大きさ
単独 又は 関連 形体	〃	線の 輪郭度		理論的に正確な寸法によって定められた幾何学的に 正しい輪郭からの線の輪郭の狂いの大きさ
〃	〃	面の 輪郭度		理論的に正確な寸法によって定められた幾何学的に 正しい輪郭からの面の輪郭の狂いの大きさ
関連 形体	姿勢 公差	平行度		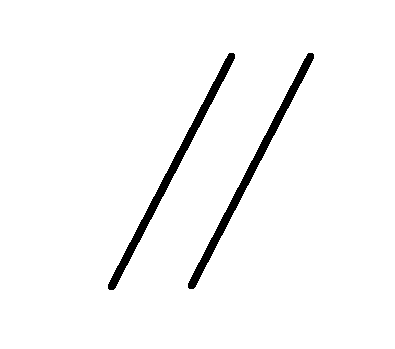データム直線、データム平面に対して平行な幾何学的直線 または幾何学的平面からの平行であるべき直線形体 又は平面形体の狂いの大きさ
〃	〃	直角度		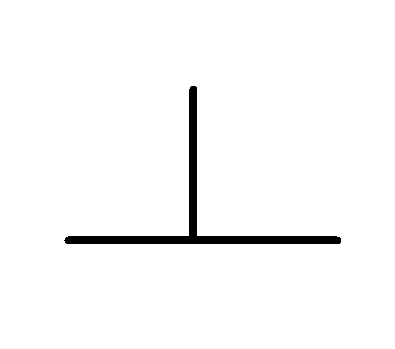データム直線、データム平面に対して直角な幾何学的直線 または幾何学的平面からの直角であるべき直線形体 又は平面形体の狂いの大きさ
〃	〃	傾斜度		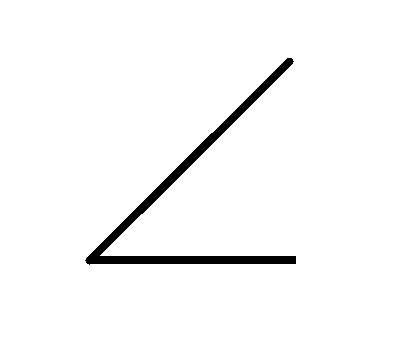データム直線またはデータム平面に対して理論的に 正確な角度をもつ幾何学的直線または幾何学的平面からの 理論的に正確な角度を持つべき直線形体及び平面形体の 狂いの大きさ
〃	位置 公差	位置度		データム直線または他の形体に関連して定められた理論的に 正確な位置からの点、直線形体または平面形体の狂いの大きさ
〃	〃	同軸度※1		データム軸直線と同一直線上にあるべき軸線の データム軸直線からの狂いの大きさ
〃	〃	同心度※1		データム円中心と同一中心上にあるべき点の データム円中心からの狂いの大きさ
〃	〃	対称度		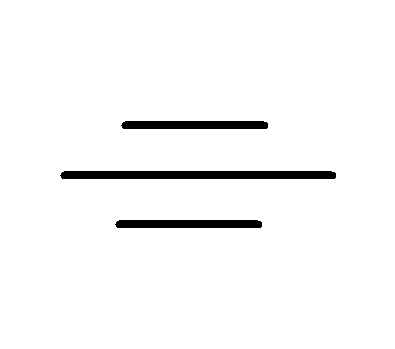データム軸直線又はデータム中心平面に関して互いに 対称であるべき形体の対称位置からの狂いの大きさ
〃	振れ 公差	円周 振れ		データム軸直線を軸とする回転面を持つべき対象物 又はデータム軸直線に対して垂直な円形平面であるべき 対象物をデータム軸直線の周りに回転したとき、 その表面が指定した位置又は任意の位置で指定した 方向に変位する大きさ
〃	〃	全振れ		データム軸直線を軸とする回転面をもつべき対象物 又はデータム軸直線に対して垂直な円形平面であるべき 対象物をデータム軸直線の周りに回転した時、 その表面が指定した位置又は任意の位置で指定した 方向に変位する大きさ

※1　同軸度と同心度の幾何公差記号は同じ◎を使います。

幾何公差－単体形体の書き方

幾何公差を図面に記入する場合は決まりがあります。単体形体の場合、対象を矢印で示して長方形の中に公差の内容（幾何公差の記号、許容値）を書き込みます。

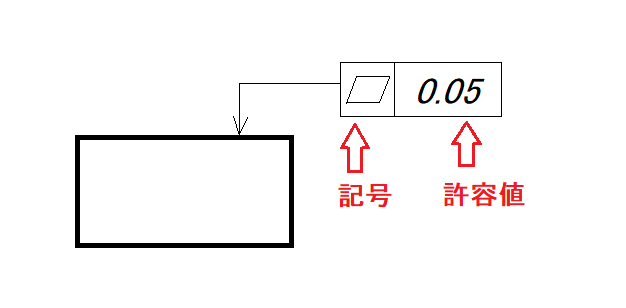
この場合だと幾何公差は平面度で許容値は0.05なので、「上面の平面度は0.05までの誤差なら許されます」という意味になります。

幾何公差－関連形体の書き方

関連形体の場合、基準（データム）に対しての公差になるので、データムを指定して、単体形体にデータム記号を加えます。

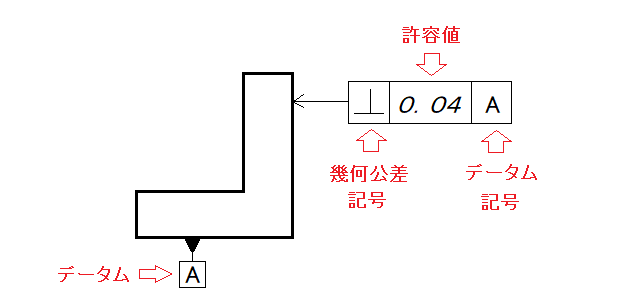
上の図の例だと幾何公差は直角度で許容値は0.04、データム面Aは下面なので、「右側の面は下面Aに対して直角度、0.04までの誤差なら許されます」という意味になります。

データムについて

関連形体の幾何公差を書くとき、多くの場合は１つのデータムを指定しますが、2つ以上のデータム記号を使う場合もあります。共通データムとデータムの優先順位について説明します。

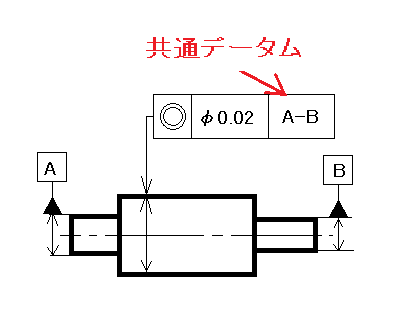
共通データムは下の図はのように2つのデータム A と B をハイフンでつなぎ一つのデータムとして扱います。こうすることで、A と B の軸の中心線をつないだ線がデータム線となります。

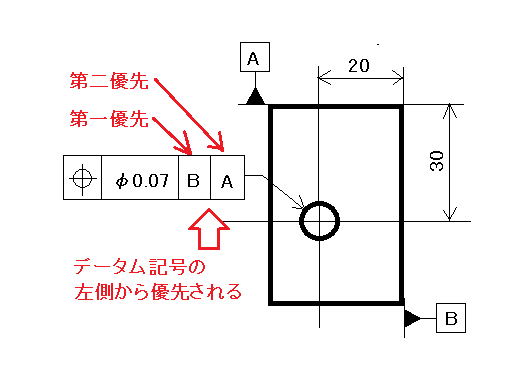
データムの優先順位は下の図のようにデータム記号の記入欄に複数のデータム記号が記入されている場合は左から優先されます。図の例だと、データム面Bが優先されます。この書き方で設計者がどこを優先させたいかを表現できます。

形状公差

公差の種類ごとに説明します。

真直度

「真っ直ぐの正確さ」です。直線精度なので、「曲がりがないよに加工してください」ということです。直線上の高い所と低い所の差を測定します。

平面度

「平面の凸凹の状態」です。最も高い点と低い点の差を測定します。

真円度

「まんまるの正確さ」です。円の径を円周に沿って測定し、最大値と最小値の差が真円度です。

円筒度

「円が真っ直ぐに正確か」です。真円度の測定を円筒状にも行い、その差が円筒度です。

線の輪郭度

「曲面の輪郭線の正確さ」です。任意の断面の輪郭線が対象です。

面の輪郭度

「曲面の輪郭面の正確さ」です。断面全体が対象です。

姿勢公差

姿勢公差の値には平面度も含まれます。
姿勢公差（平行度、直角度、傾斜度）の公差の値が仮に 0.1 だとすると、公差を指定した面の平面度が0.1より大きい場合はその時点で公差から外れることになります。

平行度

「基準となる面や線（データム）に対して平行の正確さ」です。

直角度

「基準となる面や線（データム）に対して直角の正確さ」です。公差の値の単位はmmです。

傾斜度

「基準となる面や線（データム）に対して傾斜の正確さ」です。傾斜は90°以外の角度で、公差の値の単位はmmです。

位置公差

位置度

「基準（データム）からの位置の正確さ」です。

同軸度

「基準軸（データム線）と公差対象の軸がズレていないか」です。

同心度

「基準（データム）の中心点と公差対象の中心点がズレていないか」です。
※幾何公差の記号は同じですが、同軸度は軸（線）で同心度は（点）です。

対称度

「基準（データム）に対して対称であるか」です。

振れ公差

円周振れ

「基準（データム）軸で部品を回転させたときの任意の位置の振れ」です。

全振れ

「基準（データム）軸で部品を回転させたときの全範囲の振れ」です。

まとめ：【機械製図の幾何公差】

機械製図の公差は3つに分類されます。

• 寸法公差
• はめあい公差
• 幾何公差

幾何公差には単独形体、関連形体があります。

• 単独形体には形状公差があります。
  • 形状公差・・・真直度、平面度、真円度、円筒度がありがとうございます。
• 単独形体又は関連形体
  • 形状公差・・・線の輪郭度、面の輪郭度
    
• 関連形体には姿勢公差、位置公差、振れ公差があります。
  • 姿勢公差・・・平行度、直角度、傾斜度
  • 位置公差・・・位置度、同軸度、同心度、対称度
  • 振れ公差・・・円周振れ、全振れ

データムとは関連形体で指定する基準（相手）のこと。

いかがでしたか？
幾何公差はとても便利ですが、必要以上に図面に書き込むと加工に時間がかかってしまいます。また、加工者が幾何公差を無視した部品を作ると組立の時に問題が発生してしまいます。設計者と加工者が適切な知識を持たないと、うまく仕事が回らないと思います。ぜひこの機会に基本を身に付けてください。

以上で終わりです。
最後まで読んでいただきありがとうございました。