三角関数は機械加工でよく使います。
CADやNC装置で計算することもできますが、図面を見て関数電卓でササっと計算できる仕事がはかどります。
この記事は
そういう人に三角関数を丁寧に説明します。
最後まで読んでいただくと、「機械加工で必要な三角関数や三平方の定理を使った計算」ができるようになります。
三角比の求め方
三角比は直角三角形の辺の長さの比のことで、機械加工でよく使います。
「sin(サイン) cos(コサイン) tan(タンジェント)」と「三平方の定理」を説明します。
※水平な辺をx 垂直な辺をy 斜めの辺をr
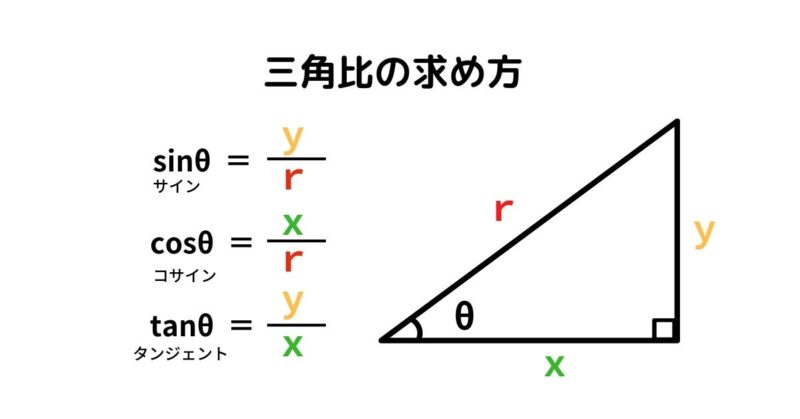
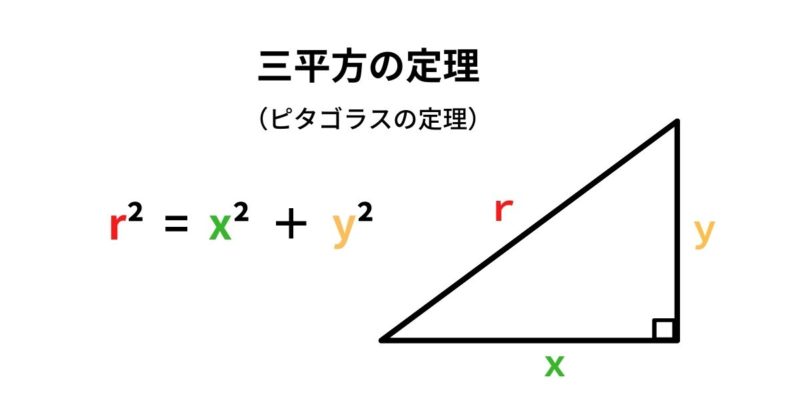
4つの公式が使えれば、機械加工では大部分の計算ができます。
三角比の覚え方
三角比の暗記には有名な方法があるので、紹介します。
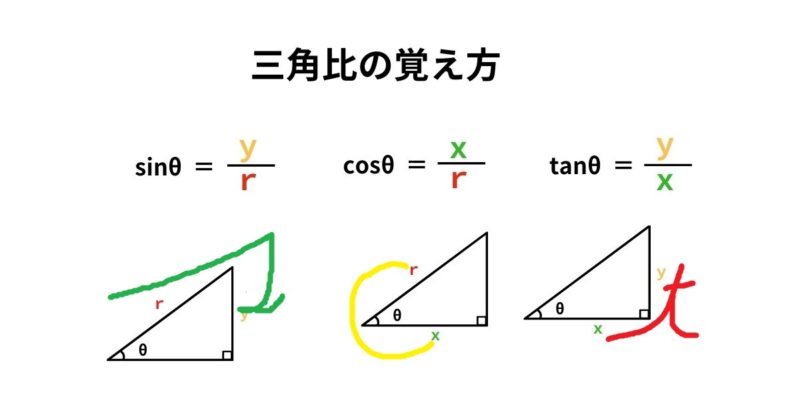
直角三角形の辺、角度の求め方
sin、cos、tan、三平方の定理を知っていれば、直角三角形は、「2辺の長さ」か、「1辺の長さと直角以外のもう一つの角度の大きさ」が分かっていれば残りの辺、角度はすべて計算できます。
最初の sin θ = y / r を使って y を求めるときは y= の形に変換します。
sinθ=y/r
sinθ×r=(y/r)×r → 両辺にrをかける
sinθ×r=(y/r)×r →右辺はrが通分できる
sinθ×r= y
y=r× sinθ
式の変換をまとめておきます。
三角比の分母を求める場合は掛け算、分子を求める場合は割り算になります。
| 三角比 | 角度 | 掛け算(分母を求める) | 割り算(分子を求める) |
| サイン | sinθ =y÷r | y=r× sinθ | r=y÷ sinθ |
| コサイン | cosθ=x÷r | x=r× cosθ | r=x÷ cosθ |
| タンジェント | tanθ=y÷x | y=x× tanθ | x=y÷ tanθ |
三角比を角度に変換したい場合は逆三角関数を使います。
- arcsin( sin−1、アークサイン)
- arccos( cos−1、アークコサイン)
- arctan( tan−1、アークタンジェント)
例)sin30° = 0.5 ↔ sin−1 0.5 = 30°
| 三平方の定理 | 半径 | 横 | 縦 |
| 式 | r²=x²+y² | x²=r²-y² | y²=r²-x² |
2乗をとるには平方根(√)を使います。
√r²=√(x²+y²) → r=√(x²+y²)
角度について
基本的な平面の直線、円での角度の性質について説明します。中学数学の復習です。
三角形の内角の和は180°で、直角三角形の場合は一つは90°なので、残りの一方の角度が θ とすると最後の角度は「90°-θ」で計算できます。
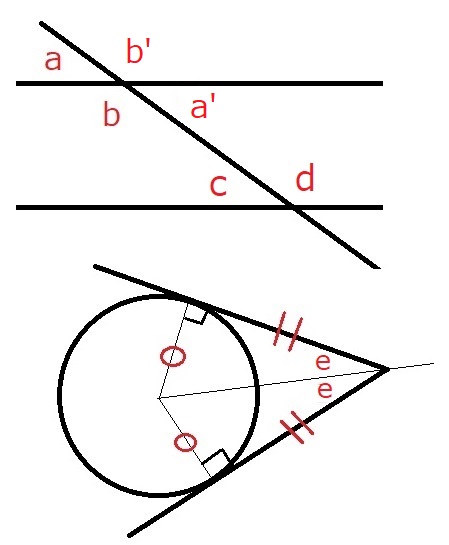
図中の角度aa’とbb’のように向かい合っている角を対頂角といい同じ大きさの角度になります。
角度aとc、b’とdのような同じ位置にある角を同位角といい、平行な直線の場合等しい角度になります。
角度a’とc、bとdのような交差する位置にある角を錯角といい、平行な直線の場合等しい角度になります。
円とそれに接する線(接線)は接点と円中心までの直線は接線に対して直線になります。
円に対して、2本の接線が交わるとき、図のように円中心と接線の交点との直線を引くと同じ大きさの直角三角形が2つできます。
機械加工で三角関数を使う例
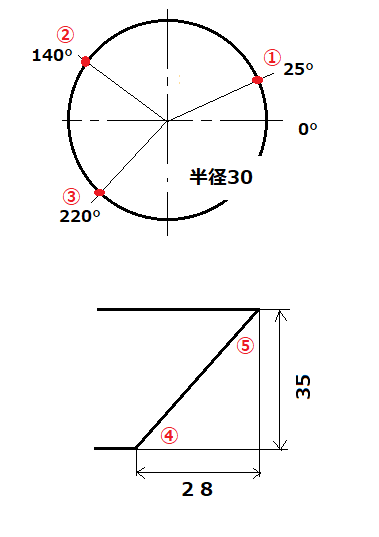
円周上の点の計算、円中心を基準とした距離
① 30×cos25 = 27.189(x)
30×sin25 = 12.679(y)
② 30×cos140 = -22.981(x)
30×sin140 = 19.284(y)
③ 30×cos220 = -22.981(x)
30×sin220 = -19.284(y)
角度の計算
④ tan−1 ( 35÷28 ) = 51.3402°
➄ tan−1 ( 28÷35 ) = 38.6598°
又は 90° – 51.3402° = 38.6598°
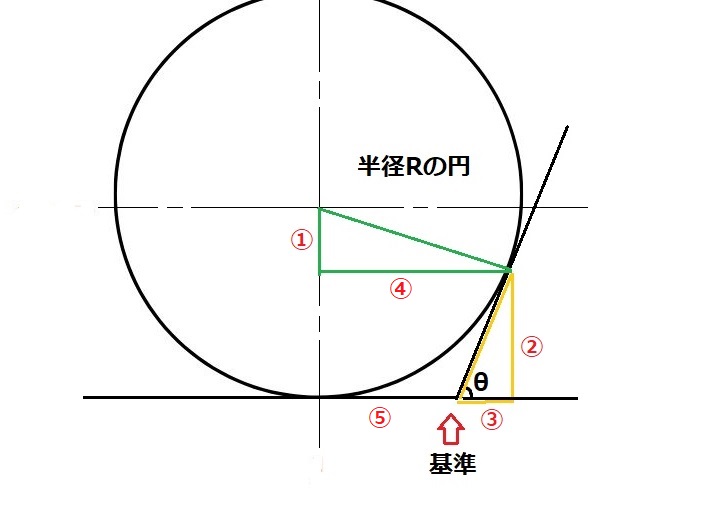
連続する2直線のコーナーにRを付ける場合
直線の交点(基準)からの円との接点まで距離、② ③ ➄ を求めます。
※角度は θ のみ使います。
- 緑の三角より ①=R×cosθ
- ② = 半径 R -①
- 黄の三角より ③ = ② ÷ tanθ
- 緑の三角より ④= R × sinθ
- ④-③=⑤
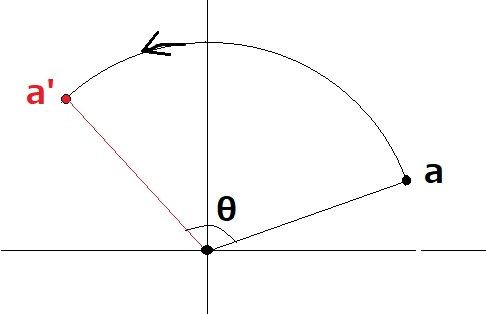
座標を回転
a点(x、y)を θ° 回転させた点をa’点(x’、y’)求める場合。
- 原点からa点の直線距離を三平方の定理で求めます。
①=√(x²+y²) - 同じく原点からa点の角度をa点の座標からアークタンジェントで求めます。
②=tan−1 ( y÷x ) - 2 で求めた角度にθを足して最初の 1 で求めた直線距離にサイン、コサインで座標を求めることができます。
x’=① × cos ( θ + ② )
y’=① × sin ( θ + ② )
この方法は手順が多いため計算が面倒です。
簡単に求める公式があるので紹介します。
x’ = x cosθ – y sinθ
y’ = x sinθ + y cosθ
さっぱりした式になりますね。
まとめ :【三角関数】機械加工でよく使う計算方法を説明します
三角比
角度、辺の長さの計算ができる。
- sin θ = y ÷ r
- cos θ = x ÷ r
- tan θ = y ÷ x
三角比を角度に変換したい場合は逆三角関数を使います。
三平方の定理
2辺がわかっていて、3辺の長さが知りたいとき使います。
- r²=x²+y²
いかがでした?
三角関数は慣れないうちは計算した数字が「本当にあってんの?」と不安になってしまいます。先輩に聞いたり、CADで確認してみてください。
ウェブで計算支援サイトもあります。計算サイトを試したい方はこちらをどうぞ。
私が使っている関数電卓です。⇓
最後まで読んでいただきありがとうございます。
以上です。





